American Odds To Decimal Odds

actucholiaicti.netlify.com › American Odds To Decimal Odds ► ► ►

Converting American odds to European Odds. The formula to convert American moneylines to European decimals odds depends if the moneyline is expressed using a positive or negative number. Positive Numbers. To convert a positive moneyline to European decimal odds take the moneyline, divide it by 100 and then add 1. The formula is (Moneyline/100) +1.

Decimal To American Odds Converter
Converting American Odds To Decimal Odds
Convert Odds To Percentage
Gambling Calculator
How To Convert American Odds To Decimal Odds

For example, the exact mathematical equivalent of decimal odds 30 is fractional odds 29/1. However 29/1 is not used in betting markets, instead 30/1 is used, so that is what appears in this converter. For an explanation of the odds types on this table see decimal, fractional and American odds.
Ex: American odds of -120 would win $100 on a $120 bet. Decimals quote the potential return should the bet succeed, relative to the stake. If $10 is bet at odds of 4, the total returned is $40 ($10 x 4) and the potential profit is $30 ($10 x 4 minus the $10 stake). Fractional Odds.

Fixed-odds betting is a form of wagering against odds offered by a bookmaker or an individual or on a bet exchange. It involves betting on an event in which there is no fluctuation on the payout. In Australia, the practice is usually known as 'SP betting'.

Calculating fixed odds[edit]

It is customary with fixed-odds gambling to know the odds at the time of the placement of the wager (the 'live price'), but the category also includes wagers whose price is determined only when the race or game starts (the 'starting prices'). It is ideal for bookmakers to price/mark up a book such that the net outcome will always be in their favour: the sum of the probabilities quoted for all possible outcomes will be in excess of 100%. The excess over 100% (or overround) represents profit to the bookmaker in the event of a balanced/even book. In the more usual case of an imbalanced book, the bookmaker may have to pay out more winnings than what is staked or may earn more than mathematically expected. An imbalanced book may arise since there is no way for a bookmaker to know the true probabilities for the outcome of competitions left to human effort or to predict the bets that will be attracted from others by fixed odds compiled on the basis personal view and knowledge.

With the advent of Internet and bet exchange betting, the possibility of fixed-odds arbitrage actions and Dutch books against bookmakers and exchanges has expanded significantly. Betting exchanges in particular act like a stock exchange, allowing the odds to be set in the course of trading between individual bettors, usually leading to quoted odds that are reasonably close to the 'true odds.'

'The best of it'[edit]

In making a bet where the expected value is positive, one is said to be getting 'the best of it'. For example, if one were to bet $1 at 10 to 1 odds (one could win $10) on the outcome of a coin flip, one would be getting 'the best of it' and should always make the bet (assuming a rational and risk-neutral attitude with linear utility curves and have no preferences implying loss aversion or the like). However, if someone offered odds of 10 to 1 that a card chosen at random from a regular 52 card deck would be the ace of spades, one would be getting 'the worst of it' because the chance is only 1 in 52 that the ace will be chosen.

In an entry for L'Encyclopédie (the Enlightenment-era 'French Encyclopedia'), Denis Diderot cites a similar example in which two players, Player A and Player B, wager over a game of dice that involves rolling two six-sided dice. Player A wins if the dice add up to 12, of which there is only one possible case. Player B wins if the dice fall in any other combination, of which there are 35 possibilities.^[1] It is mathematically disadvantageous to make a bet if one gets'the worst of it.' Accordingly, for the bet to be 'fair,' the amount each player could potentially lose or gain from the wager should be adjusted, depending on the odds of their success.

Laying odds[edit]

When making a bet in which one must put more at risk than one can win, one is laying the odds. Rational bettors will do so only if the actual chances of an adverse outcome are low enough that the expected outcome even after deduction of taxes and any transaction costs is favorable to the person placing the bet. For example, if one bets $1,000 that it will rain tomorrow and can win only $200 but can lose the entire $1,000, one is laying odds that will rain tomorrow. Laying odds is reflected in the colloquial expression '[I would] dollars to doughnuts' — with which the speaker is expressing a willingness to risk losing something of value in exchange for something worthless, because winning that bet is a certainty.^[2]

Lay betting[edit]

'Lay betting' is a bet that something will not happen, so 'laying $50 on a horse' is betting the horse will not win. Bookmakers sell bets based on the odds of a specific outcome, but lay betting allows the bettor (in some English-speaking countries, the 'punter') to reverse roles with the bookmaker, using odds to sell the opposite outcome to the bookmaker. In this context, 'lay' is used in the sense of 'layman', i.e., a bet sold by someone who does not sell bets professionally.

Types of odds offered[edit]

There are three widely used means of quoting odds:

Fractional odds[edit]

Favoured by bookmakers in the United Kingdom and Ireland and common in horse racing, fractional odds quote the net total that will be paid out to the winning bettor relative to the stake. The term 'fractional odds' is something of a misnomer, especially when visually reinforced by using a slash (as opposed to, e.g., a colon or the word 'to' or 'on') to separate a potential gain from the amount that a bettor must wager in order to receive it upon a win, because the 'fraction' in question represents not the odds of winning or even the reciprocal of the odds of winning but rather the fraction (for any odds longer than 'even money' or chances of winning less than 50%, an improper fraction) of the amount at stake that the upside outcome represents. This fraction may be derived by subtracting 1 from the reciprocal of the chances of winning; for any odds longer than 'even money,' this fraction will be an improper one.^[3]^[4] Odds of 4:1 ('four-to-one' or less commonly 'four-to-one against') would imply that the bettor stands to make a £400 profit on a £100 stake. If the odds are 1:4 (read 'one-to-four', or alternatively 'four-to-one on' or 'four-to-one in favor'), the bettor stands to make £25 on a £100 stake. In either case, against or on, should he win, the bettor always receives his original stake back, so if the odds are 4:1 the bettor receives a total of £500 (£400 plus the original £100). Odds of 1/1 are known as evens or even money.

Not all fractional odds are traditionally read using the lowest common denominator. Perhaps most unusual is that odds of 10:3 are read as 'one-hundred-to-thirty'.

Fractional odds are also known as British odds,UK odds,^[5] or, in that country, traditional odds.

Decimal odds[edit]

Favoured in Continental Europe, Australia, New Zealand and Canada, decimal odds differ from fractional odds by taking into account that the bettor must first part with their stake to make a bet; the figure quoted, therefore, is the winning amount that would be paid out to the bettor.^[4]^[6] Therefore, the decimal odds of an outcome are equivalent to one plus the decimal value of the fractional odds; in the absence of built-in house advantage to cover overhead, profit margins, or (for an illegal enterprise) compensation for the fact that both chances of prosecution and penalties in the event of conviction tend to be higher for bookmakers than for clients, the decimal odds associated with a given outcome would be the decimal expression of the reciprocal of what the offering party assesses to be the outcome's chance of occurring.^[7] Thus, even odds 1/1 are quoted in decimal odds as 2. The 4/1 fractional odds discussed above are quoted as 5, while the 1/4 odds are quoted as 1.25. It is considered to be ideal for parlay betting because the odds to be paid out are simply the product of the odds for each outcome wagered on.

Decimal odds are also known as European odds, digital odds or continental odds and tend to be favoured by betting exchanges because they are the easiest to work with for trading, in this case the purchase and sale of upside and downside risk.^[5]

Moneyline odds[edit]

Moneyline odds are favoured by United States bookmakers and as such are sometimes called American Odds.^[4] There are two possibilities: the figure quote can be either positive or negative. Moneyline refers to odds on the straight-up outcome of a game with no consideration to a point spread.

Positive figures: If the figure quoted is positive, the odds are quoting how much money will be won on a $100 wager (done if the odds are better than even). Fractional odds of 4/1 would be quoted as +400 while fractional odds of 1/4 cannot be quoted as a positive figure.

Negative figures: If the figure quoted is negative, the moneyline odds are quoting how much money must be wagered to win $100 (this is done if the odds are worse than even). Fractional odds of 1/4 would be quoted as −400 while fractional odds of 4/1 cannot be quoted as a negative figure.

Even odds: Even odds are quoted as +100 or −100. Some but not all bookmakers display the positive symbol.

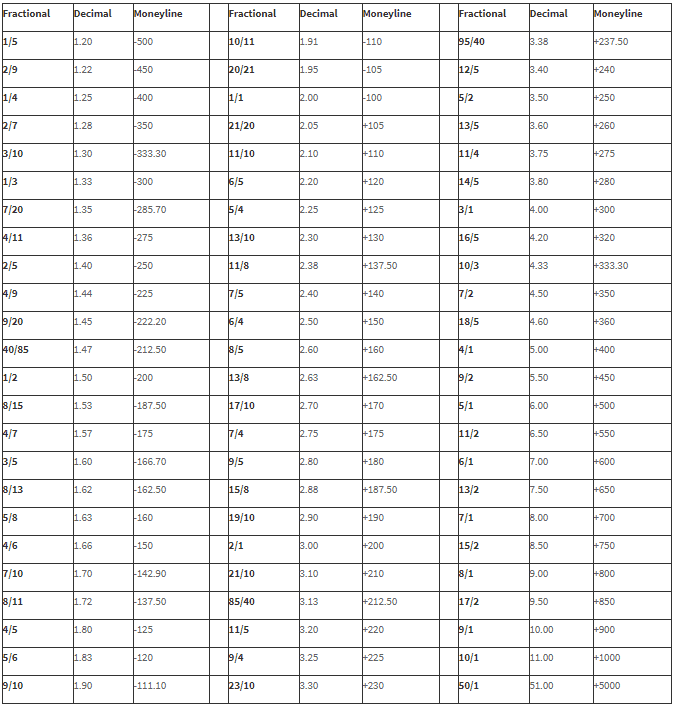
Odds conversion[edit]

To convert fractional odds to decimal, take the fractional number, convert it to decimal by doing the division, and then add 1. For example, the 4-to-1 fractional odds shown above is the same as 5 in decimal odds, while 1-to-4 would be quoted as 1.25.

The method for converting moneyline to decimal odds depends on whether the moneyline value is positive or negative. If the moneyline is positive, it is divided by 100 and add 1. Thus, +400 moneyline is the same as 5.0 in decimal odds. If the moneyline is negative, 100 is divided by the absolute moneyline amount (the minus signed is removed), and then 1 is added. For example, −400 moneyline is 100/400 + 1, or 1.25, in decimal odds.

Decimal	Fractional	Moneyline	Win% (to break even)	Return (minus stake)
1.01	1/100	−10,000	99.01%	1.00%
1.11	1/9	−900	90.00%	11.11%
1.33	1/3	−300	75.00%	33.33%
1.50	1/2	−200	66.67%	50.00%
2.00	1/1	±100	50.00%	100.00%
3.00	2/1	+200	33.33%	200.00%
4.00	3/1	+300	25.00%	300.00%
10.00	9/1	+900	10.00%	900.00%
101.00	100/1	+10,000	0.99%	10,000.00%
${displaystyle x+1,}$	${displaystyle x,}$	${displaystyle -{frac {100}{x}}}$	${displaystyle {frac {100}{x+1}}%}$	${displaystyle left(100xright)%}$
${displaystyle x+1,}$	${displaystyle x,}$	${displaystyle +100x,}$	${displaystyle {frac {100}{x+1}}%}$	${displaystyle left(100xright)%}$

References[edit]

^'Wager'. University of Michigan Library. Retrieved 1 April 2015.
^Listening to America, Stuart Berg Flexner (Simon and Schuster, New York, 1982).
^'Betting School: Understanding Fractional & Decimal Betting Odds'. Goal. 10 January 2011. Retrieved 27 March 2014.
^ ^a^b^cCortis, Dominic (2015). Expected Values and variance in bookmaker payouts: A Theoretical Approach towards setting limits on odds. Journal of Prediction Markets. 1. 9.
^ ^a^b'Betting Odds Format'. World Bet Exchange. Archived from the original on May 2, 2014. Retrieved 27 March 2014.
^D., Chris. 'What is Fixed odds betting and Due Column betting?'. TBR. Retrieved 27 March 2014.
^'Fractional Odds'. betstarter.com/. Archived from the original on April 2, 2014. Retrieved 27 March 2014.

External links[edit]

Retrieved from 'https://en.wikipedia.org/w/index.php?title=Fixed-odds_betting&oldid=1004157818'

The simplest sports betting math many punters possess is the ability to convert odds and calculate break even percentages, also known as implied probabilities. After spending years doing these calculations, first on a windows calculator, and later in an excel spread sheet, I finally developed the Online Gambling odds converter you’ll find below.

Odds Converter Tool

[oddscalc]

In case you’re not familiar with the difference between American Odds called moneylines and European odds, which are in decimal format, here is how each works.

American Odds

Also known as moneylines, are offered as either a positive or negative number. When positive, the moneyline represents how much profit a punter stands to make on a $100 stake. To give an example, a line of +125 represents risk $100 to win $125 profit. Negative moneylines represent how much a punter needs to stake for a winning bet to profit $100. A moneyline of -235 is risk $235 to win $100 profit.

European Odds

Also known as decimal odds, represent how much a winning ticket is worth for each dollar staked. For example if a punter wagers $10.00 at odds 1.95 and wins, their payout is $10 x 1.95 = $19.50. A major difference between American and European odds is that while the American version is based on profit, the European version is based on return. Likewise, a $10 wager on odds 1.95 translates to risk $10.00 to potentially profit $9.50. Considering 1.95 pays less than even money, it would be expressed in American odds format as a negative moneyline.

The best way to convert American odds to European format, and vice versa, is to use the “odds converter” located above. For those of you interested in the math, I’ll cover it great detail later in this article. First let me discuss break even percentage and implied probability.

Implied Probability

Is how often a bet must win for it to have neutral value. To give the simplest example, take American odds +100 (which is the equivalent of 2.00 in European odds) where winning bets are paid even money, here the implied probability is 50%. This is because in American format risk $100 to win $100, and in European format stake $1 to return $2, you’ll need to win an average of 50% of the time to break even over the long haul.

Where our odds converter comes in handy is let’s say you’ve done an analysis on a game between the Boston Red Sox and Tampa Bay Rays and determined the Red Sox should be 57% favorites in this game. After price shopping, the best odds you can find on the Red Sox are -128, which in European format is 1.781. There are now two ways you can determine if you’ve found a good bet. The first method is to plug 57% into our odds converter under the required break even field. Doing this you’ll find at 57% the true odds in American format are -132.6 (1.754 European). Consider you’re getting better than this with the -128 (1.781 European) you have a profitable bet.

The second way you could approach the above problem, is to plug -128 into our odds converted under American odds. Here you’ll see the required break even rate (implied probability) is 56.14%. Considering your calculation of a 57% win probability comes out higher than the win rate needed to break even, you’ve find yourself a good bet.

Sports Betting Strategy You Should, but Most Don’t, Understand

For those with basic sports betting math skills, the sample problem I’m about to give will be easy to solve. If you’re stumped, or answer incorrectly, what you’re about to read could very well be what gets you on the path required to winning consistently at sports betting.

The sample

Decimal To American Odds Converter

Every online betting site with odds on a NBA basketball game between the Orlando Magic and Sacramento Kings has the odds listed in American format as Magic -545 / Kings +445.

Someone comes long and says “I’ll offer you either Magic -490 or Kings +490, your choice”. Which of these options, if any, has the highest expected value?

The way many sports bettors would approach this is to average out 545 and 445 and figure the fair value is about -495 / +495. Using this failed logic they’d end up taking the Magic -490 as that’s better than the fair price and must be +EV. The problem is neither American nor European odds work this way; they can’t be averaged out to calculate the fair value.

The first step those who understand sports betting math take to solve this problem is the conversion of Magic -545 / Kings +445 to break even percentages.

After plugging the odds into our odds converted I find:

Magic -545 = 84.50% required break even percentage
Kings +445 = 18.35% required break even percentage.
Adding these together you’ll find they total 102.85%. They total more than 100% because juice, which is how the bookmakers profit, is included in the -545/+445 lines. To remove juice we divide each by 102.85%.

Magic -545 = 84.50%/102.85% = 82.16%
Kings +445 = 18.35%/102.85% = 17.84%

To check double check our math 82.16 + 17.84% = 100%. We’ve successfully removed the juice and now have each team’s no-vig win probability.

Next go back to our odds converter and plug in the no vig win probabilities into the field titled “required break even %. Doing this we see:

Magic at 82.16% = -460.5 in American odds format.
Kings at 17.84% = +460.5 in American odds format.

The offer we were given was Magic -490 or Kings +490 and we calculated the fair prices with no vig are Magic -460.5 and Kings +460.5. The obvious best bet from +EV/-EV standpoint here is Kings +460.5.

The beautiful thing about sports betting, there are dozens of sites each with unique lines on the same game. If you’re able to gauge the consensus line by looking at what the discount bookmakers and exchanges such as Pinnacle, 5Dimes, and Betfair are offering, when you spot a line that is off at a recreational betting site such as Sportsbook.com, Bodog, or Intertops, you’ll have no problem calculating which side if any is a profitable long term bet. The ability to do this alone, combined with bonuses and promotions is enough for the average sports bettor to make some serious extra coin each season. With that said, be sure to bookmark this page so you have quick access to our odds converter as it’s a tool serious sports bettors will want to use often.

Math to Convert Betting Odds

To conclude this article I’ll share the math involved in converting odds and break even percentages. Remember our odds converter can do this math for you at the click of a button.

Converting American odds to European Odds

The formula to convert American moneylines to European decimals odds depends if the moneyline is expressed using a positive or negative number.

Positive Numbers

To convert a positive moneyline to European decimal odds take the moneyline, divide it by 100 and then add 1. The formula is (Moneyline/100) +1. To give an example, the math to convert +358 is (358/100) +1 which calculates to European odds of 4.580.

Negative Numbers

Converting American Odds To Decimal Odds

To convert a negative moneyline to European decimal odds take 100 divide it by the moneyline (without using the negative sign) and then add one. The formula is (100/Moneyline) + 1. To give an example, the math to convert -115 is (100/115) +1 which calculates to European odds of 1.870.

Converting European Odds to American Odds

The formula to convert European odds (decimals) to American moneyline format depends if the odds are 2.00+, or 1.999 or less.

Odds $2.00+

To convert European decimal odds 2.00 or greater to an American moneyline the math is: 100*(Decimal odds -1). For example, odds 2.183 use the formula 100*(2.183-1) which calculates to an American moneyline of +118.3.

Odds Under $2.00

To convert European decimal odds less than 2.000 to an American moneyline the math is (-100)/(Decimal odds – 1). For example, odds 1.71 uses the formula -100/(1.71 -1) which calculates to an American moneyline of -140.8.

Calculating Break Even Percentage

When dealing with European decimal odds, calculating how often a bets must win to break even is simple division. The formula is (1/odds=%). To use decimals odds 2.15 as an example, the math is 1/2.15 which equals 0.4651; converted to a percentage this is 46.51%. That’s how often a bet at 2.15 must win to have neutral value and is referred to as its break even rate or implied probability.

When dealing with American odds the formula to calculate a bets required break even rate (implied probability) is risk/return=implied probability, where return is how much a winning ticket would pay. For example at -215 a sports bettor wagers $215 to win $100, a winning bet returns $315 (the $215 stake and $100 win). In this case the math to calculate implied probability is 215/315 which equals 0.6825 and as an implied probability is 68.25%.

Converting Win Probabilities to Fair Odds

In cases where you know a team is going to win a certain percentage of the time and you’re looking to convert this percentage into fair European decimal odds or an American moneyline, this can be done with simple math. First change your percentage to a decimal (example 50.5% is 0.505) then use the formula (1/probability=European Odds). In the case of 50.5% the math is 1/.505 which equals European decimal odds of 1.98. To convert this to American odds go back to our formula (-100)/(Decimal odds – 1) which calculates to a moneyline of -102. As a reminder, in cases where the decimal odds are 2.0 or greater the moneyline will come out a positive number and therefore the conversion formula is 100*(Decimal odds -1) instead of the (-100)/(Decimal odds – 1) used in this example.

Convert Odds To Percentage

Best Online Betting Odds

Gambling Calculator

Now that you understand how to calculate odds, you’ll likely appreciate how impressive the odds offered at www.5dimes.eu are. While no doubt the most popular reduced juice option for American players, 5Dimes also offers soccer, cricket, Euro hockey, Rugby League, Rugby Union, Aussie Rules, volleyball, motor racing, golf, tennis, snooker, water polo and darts at better odds than High Street bookmakers and TAB. To learn more read our 5Dimes Review.

How To Convert American Odds To Decimal Odds

Of course, the best advice we can give you at Online Gambling is to keep learning sports betting math, while using dozens of accounts to shop lines. We hope you enjoyed this article on converting odds, and wish you the best of luck this sports betting season.